Blog: The use of synthetic or external data in clinical trials

Blog by: Kert Viele

External or synthetic data aspires to shorten clinical trials, saving resources while maintaining scientific accuracy. Like any aspiration, external data may fall short of this goal. In this post we will discuss

1. The tradeoff between saving patient resources and maintaining scientific robustness
2. How this tradeoff amplifies when using external/synthetic data more aggressively
3. Show a numerical example of these tradeoffs
4. Discuss the assumptions needed for a specific method’s benefits to exceed its risks.

The tradeoff

Standard experiments enroll a set of patients and randomize between a control and treatment arm. For many experiments, external or synthetic data may be available on the control or, less commonly, the treatment arm. Standard trials ignore this external information, but we could also use it either to augment randomized controls within a trial or to replace the control arm altogether.

Using external data may save patient resources, but also carries the risk of degraded trial performance. The risks and benefits of using external information depend on the agreement between the synthetic data and the actual trial. Do the synthetic data very closely emulate the current trial, or are there systematic differences? If the agreement is good, the external information is valuable and can be used to save patient resources and/or improve inferential performance. If the agreement is poor, we obtain biased estimates of treatment effects and poor inferential performance on statistical tests. We will approve more ineffective therapies and miss more effective ones. While this post largely takes a frequentist perspective, reflecting current regulatory guidance, the calculation can be redone in terms of Bayesian utilities with similar qualitative conclusions. In the Bayesian framework one’s prior beliefs about the agreement are key to selecting the appropriate use of the external/synthetic information.

What is “good” or “poor” agreement depends on how we use the external data. Aggressive use of external data can result in large patient savings but requires a very high degree of agreement. More conservative use of external data results in smaller patient savings but is beneficial with more limited amounts of agreement. Single arm trials are particularly aggressive use of external data, and thus come with strong assumptions.

A numerical example

Suppose we are designing a trial with a dichotomous (yes/no) outcome. We expect controls to have a 60% rate and hope our novel treatment obtains a 75% rate. A standard trial might enroll N=150 (ish) on each arm, obtaining 2.5% one sided type 1 error and 80% power. Suppose we can also obtain N=150 synthetic controls.

We could simply replace our current controls with these N=150 synthetic controls. This will save us 50% of the required patient resources. For this trial, we can quantify the levels of agreement where we achieve inferential benefits and risks. In the figure, the x-axis is “agreement”, the difference between the external/synthetic data and the current trial control parameter. If the synthetic data indicates a 58% response rate, while in truth (unknown) the control arm would have had a 62% response rate, then the difference (x-axis) would be 0.58-0.62 = (-0.04).

The figure shows the type 1 error and power (y-axes) of our “replace control” trial (black curves) as a function of agreement. When we have perfect agreement and the difference is 0, our trial obtains 2.5% type 1 error and 80% power. We save our 50% patient resources at no inferential cost. When the synthetic controls are lower than our would-be current controls, it makes the trial easier to win (like running hurdles with lower hurdles). This increases our power but increases our type 1 error. If the synthetic controls are just 4% lower, our one-sided type 1 error exceeds 10%. This is the regulatory risk that provides most of the resistance to using external data. In contrast, if the synthetic controls are higher than current controls, the trial becomes harder to win. This doesn’t create a type 1 error risk but does dramatically lower the power of the trial. When the synthetic control is 4% higher than the current trial, our power is reduced below 55%. While type 1 error inflation often headlines the acceptability of external data, sponsors should be aware of the potential for power loss as well.

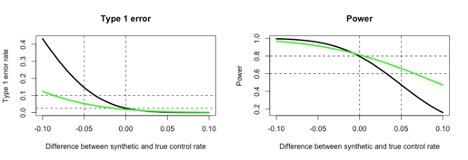
The green curves in the figure show an alternative design. Instead of fully replacing the control arm, let’s enroll N=75 concurrent controls and augment those with the N=150 synthetic controls. We will also use downweighting so that each synthetic control is weighted at 0.5 of a current control patient. This trial saves 25% of the patient resources compared to 50% savings from fully replacing the controls, but it retains randomization and concurrent controls.

Qualitatively, the green curves mirror the black curves. Type 1 error increases when the synthetic control rate is lower than concurrent controls, and power decreases when the synthetic control rate is higher. These risk increases, however, are far slower than far the “replace control” trial. Type 1 error exceeds 10% as the synthetic control rate falls 8-9% below the concurrent control, as opposed to 4%, and power is similarly dropping but maintained longer.

What assumptions might justify external data?

A strict view of type 1 error control, not allowing any potential scenario with inflated type 1 error, would preclude either use of external data. However, the FDA guidances explicitly allow external data to inflate type 1 error on a case by case basis. In practice, these discussion involve the quality of the external data, its applicability to the current trial, and an informal belief that the level of agreement will be sufficiently high that the trial will obtain good operating characteristics. Essentially “based on XX, we belief the agreement will be 5% or better, and this will keep type 1 error at or below YY”. Our current experience is that, when external data is allowed at all (again, case by case), that one sided type errors of 5-15% in the expected range of agreement are possible, with the higher values reserved for hard to research areas like rare diseases and pediatrics.

More formal assumptions are possible, and here we turn to current research. Some recent papers have generated synthetic controls for trials that enrolled concurrent controls, and then compared the synthetic and concurrent groups. Several of these papers have used standard hypothesis tests, with a finding that the synthetic and concurrent controls were not statistically different. This is a wonderful start, but I suspect we will need to go a couple more steps.

First, we need to do this in many trials, not just a few, to see a broader pattern of agreement. For example, we need to be able to draw conclusions like “agreement is likely within X% in 90% of trials”. That is a big ask, but a relevant question. Fortunately, there is no shortage of published trials with real data, and synthetic data is easier to generate than real data. Second, once we obtain a distribution of agreement, we can tailor our methodology for using external data to fit the levels of mismatch we are likely to obtain in the long run.

Suppose we found that in repeated use (many trials) differences are uniformly distributed between -5% and 5%. Clearly other distributions may be more likely, but this one is simple to think about. We can compute the long run behavior of our designs in repeated use. In the augmented control design, differences of -5% produce inflated type 1 error with higher power, while differences of 5% produce power losses with decreased type 1 error. High agreement (differences near 0) produces both type 1 error and power advantages. How does this all average out in repeated use? If the difference is uniformly distributed between -5% and 5%, the long run average type 1 error is 2.2% (just averaging the green curve within that range) while the average power is 80.3%. Thus we obtain long run gains in performance, while saving 25% of patients, compared to standard trials. Our “replace control” trial, in contrast (averaging over the black curve), has 4.3% average type 1 error and 76.5% average power. We save more patients, but at an inferential cost on both error rates.

Generally speaking, given any distribution of mismatch there is some way to use external data to generate improved inferential performance with reduced patient resources. If we know the agreement will be high (often a strong assumption) we can use the external data aggressively to large benefit. If the difference is more uncertain, we may need to use the external data conservatively. To repeat, a single arm trial with no increase in the treatment arm constitutes a very aggressive use of external data, and thus comes with very strong assumptions.

Note a fully externally controlled trial that increases sample size on active is more desirable. Suppose instead of trying to save all 150 control patients with our synthetic controls, we plan a fully synthetically controlled trial with N=225 patients on the treatment arm, and we perform our test using a 0.010 nominal one-sided type 1 error rate, instead of 0.025. Thus, we save 25% of the patients from a standard trial (same as the augmented control design) and test at a more conservative level. With this design, if differences are again uniformly distributed between -5% and 5%, we achieve an average type 1 error of 2.4%, and an average power of 81.7%. This is in line with our augmented control design, with the same sample size savings and slightly higher type 1 error rates and power.

In summary, the use of external/synthetic data is highly dependent on the expected agreement between that data and the current trial conditions, and the methodology used must match that expected agreement to achieve inferential benefit while saving sample size. It would be valuable to perform further research in accessing the levels of agreement obtained in real trials to properly calibrate these methods.